Mathematics and neurodegenerative diseases

Neurodegenerative diseases, such as Alzheimer's (AD) or Parkinson's disease (PD), are complex and multiscale phenomena. What are the primary mechanisms driving the long-term development of neurodegenerative diseases? What insights can we gain from the large volume of available patient neuroimaging data and how can this data be used in mathematical models?
Interacting proteins in neurodegenerative diseases
Brief synopsis
Some neurodegenerative diseases, such as progressive supranuclear palsy, are primarily described by the propagation of a single misfolded protein species. Others, such as Alzheimer's or Parkinson's disease, have more than one misfolded protein population; these populations can interact to exacerbate disease progression. Interaction is an important mechanism in these diseases and clinical experiments suggest a means of interaction that can be modeled mathematically and tested in silico.
What I am doing
I have developed and analyzed a model of interacting proteins in Alzheimer's disease and further examined traveling wave solutions. I also developed a high-performance scientific computing library to solve my model (movie, left) of AD on a domain created from the brain imaging data of 426 patients. I am currently working on model extensions, machine learning and inference applications coupling AD, or PD, models to patient imaging data.Clearance in neurodegenerative diseases
Brief synopsis
Clearance is a fundamental mechanism in neurodegeneration. Experiments, in mice, suggest that the failure of brain clearance systems may play a central role in neurodegenerative diseases. Using analysis and scientific computing, mathematical models of clearance can investigate human pathology where experimental results are largely unavailable.
What I am doing
Alongside experimental collaborators at Cambridge, I showed that the equations governing misfolded protein aggregation yield a critical clearance. This value mitigates the proliferation of misfolded proteins and, ultimately, the onset of neurodegenerative disease. Based on my earlier work, I am now collaborating with experimentalists, from Norway, on patient-data driven mathematical modeling investigating the effect of glymphatic clearance in AD development (movie, right).Disease staging and topology in network mathematical models
Brief synopsis
Much like disease outbreaks, neurodegenerative protein misfolding is often thought to spread from one or more epicenters within the brain. Clinical experiments suggest that important diseases, such as Alzheimer's and Parkinson's disease, spread their pathology in a structured progression, called a staging pattern, throughout the brain. It is important for mathematical models to reliably reproduce clinically observed staging behavior.
What I am doing
In a recent study, I have considered the staging problem using a Fisher-Kolmogorov model of Alzheimer's disease tauopathy. The primary conclusion is that the balance of growth and diffusion affects the correct staging but this effect is coupled with the topology of the brain graph constructed for the individual patient (movie, left). My work highlights the need for further mathematical studies of staging and for the quantification of model uncertainty introduced by clinical tractography and patient graph construction.
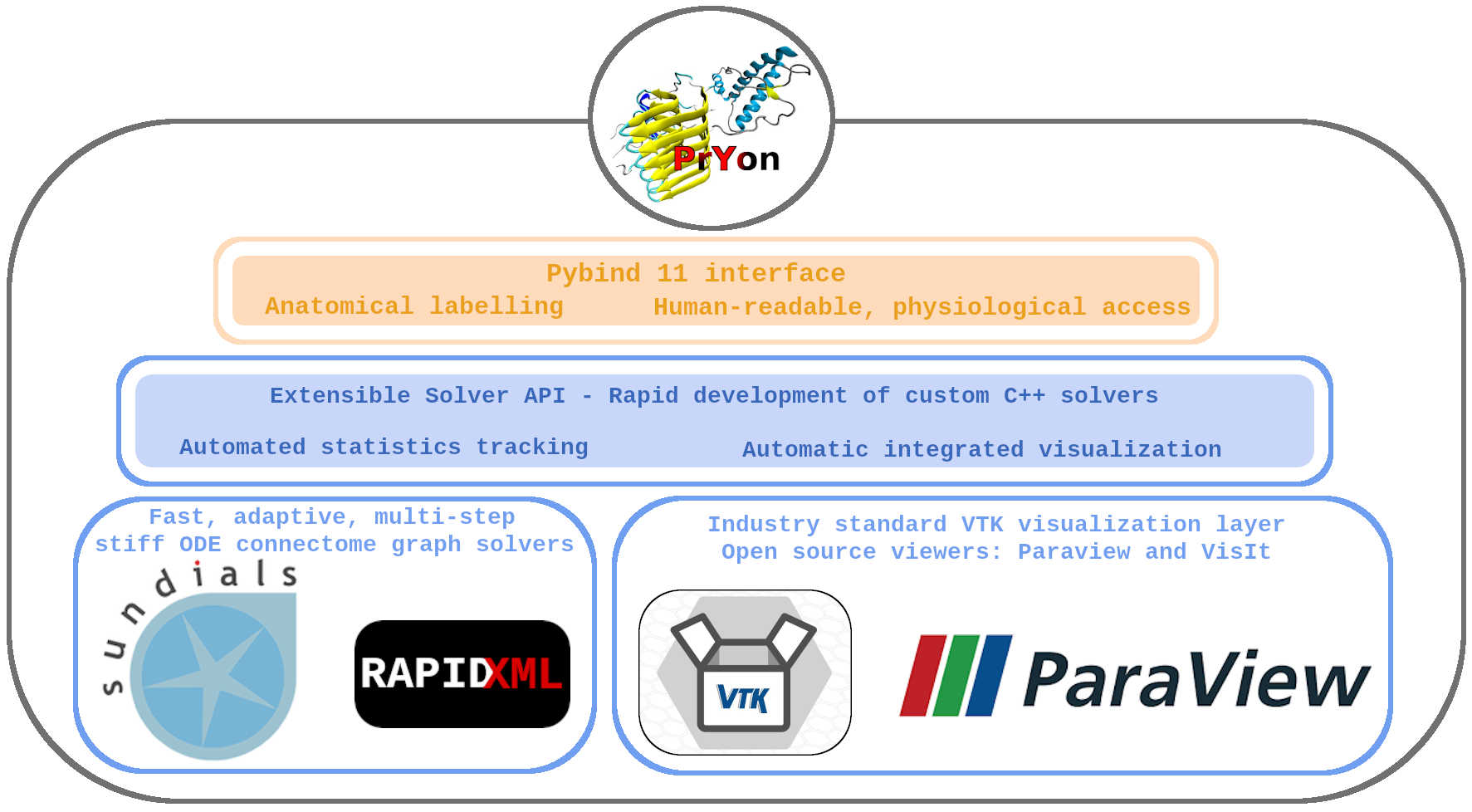
Scientific Computing and network neurodegeneration
Brief Synopsis
Over the last decade, the network neurodegeneration models typically used by clinicians have been simple diffusion systems posed on low-resolution brain graphs. More sophisticated mathematical models are coupled, stiff nonlinear systems of diffusion-reaction type. Solving modern mathematical models on high-resolution brain connectomes, in a reasonable amount of time, is out of the reach of many, if not most, in the brain research community.
What I am doing
I have developed an extensible scientific computing library for solving large, stiff mathematical models on high-resolution brain brain graphs. The library is built on the parallel, high-performance Sundials package and the VTK visualization library. I implemented, solved and visualized the models on this page using my library. PrYon is a Python version of my library; enabling easy access, for students and researchers alike, to powerful mathematical network neurodegeneration solvers that can be used alongside machine-learning methods. PrYon will be released as open-source software.